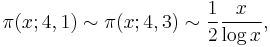Chebyshev's bias

In number theory, Chebyshev's bias is the phenomenon that most of the time, there are more primes of the form 4k + 3 than of the form 4k + 1, up to the same limit. This phenomenon was first observed by Chebyshev in 1853.

Description

Let π(x; 4, 1) denote the number of primes of the form 4k + 1 up to x. Similarly, let π(x; 4, 3) denote the number of primes of the form 4k + 3 up to x. By the prime number theorem, extended to arithmetic progression,

\pi(x;4,1)\sim\pi(x;4,3)\sim \frac{1}{2}\frac{x}{\log x},

i.e., half of the primes are of the form 4k+1, and half of the form 4k + 3. A reasonable guess would be that π(x;4,1)>π(x; 4, 3) and π(x; 4, 1) < π(x; 4, 3) each also occur 50 % of the time. This, however, is not supported by numerical evidence—in fact, π(x,4,3)>π(x;4,1) occurs much more frequently.

In general, if 0 < a,b < q are integers, (a, q) = (b, q) = 1, a is a quadratic residue, b is a quadratic nonresidue mod q, then π(x; q, b) > π(x; q, a) occurs more often than not. This has been proved only by assuming strong forms of the Riemann hypothesis. The conjecture of Knapowski and Turán, however, that the density of the numbers x for which π(x; 4, 3) > π(x; 4, 1) holds, is 1, turned out to be false. They, however, do have a logarithmic density, which is approximately 0.9959...(Rubinstein—Sarnak, 1994).

See also

References